Understanding Ship
and Boat Stability
(Stability & Trim - Part1)
By: Brian Trenhaile, P.
E., Naval Architect & Marine Engineer,
Hawaii Marine Company, revised Sept. 2017.
This article was originally published in the April/May 1998
issue
of Hawaii Ocean Industry &
Shipping News.
For the sake of just one human life, it is worth understanding how stability works. Sadly multitudes of precious lives are lost due to a lack of awareness and understanding regarding this most crucial topic.
In September of 2017 the ferry M/V Nyerere capsized in Lake Victoria, Tanzania. The latest death toll is 224, but it is possible another 100 bodies may be recovered. In 2002 an oceangoing ferry named the La Joola capsized off the West Coast of Africa between 1,034 to 1,600 crew and passengers perished in this unprecedented peace-time maritime disaster. Another recent example is the September 1997 capsizing of the Pride of Gonave in Haiti. Roughly 200 souls perished in this unfortunate debacle. In fact, stability related ferry disasters are rather common, claiming some 400 lives in Lake Victoria in May 1996; 338 lives off Sumatra in January 1996; and 852 lives in September 1994 when the ferry Estonia sank in a Baltic storm.
The ferry industry is not the only segment of the marine industry that needs to be concerned about stability. Statistically, a higher percentage of people die in commercial fishing than any other occupation in the United States. Inadequate stability is one of the most common sources of deaths in commercial fishing. Yet this industry often vigorously opposes any type of regulation regarding its vessels.
Then there are sailboats. Many of the newer boats are constructed lighter and with wider and flatter midsections to get better race performance and lower ratings. Unfortunately, these trends have proved to be deadly for the 15 sailors who perished in the 1979 Fastnet Race. Investigators were called in to find out why this race was so disastrous. They concluded that the vessels should have been narrower and heavier than they generally were. Still, these race performance enhancing trends continue. Racing sailors still go out in some of the worlds most perilous bodies of water in boats that are often even more extreme than those of the Fastnet Race.
Naturally, all segments of the marine industry need to be concerned about stability. A tow boat can trip over its tow wire, a boat lifting a load can flip itself over, and too much free surface in tanks can make a stable boat unstable. A good way to avoid being a victim of a sensational stability incident is to understand stabilitys basic concepts. Paying attention to little details, however mundane, often saves lives.
This article touches some of the more crucial aspects of this important topic, in particular some key principles regarding "static intact stability." Static intact stability involves heel angles that are restricted to less than 10 degrees and makes extensive use of the metacentric height concept.
United States Coast
Guard regulations and American Bureau of Shipping
rules will often require that a vessel have a certain amount of
metacentric height. The concepts described here are applicable to boats,
yachts, ships, and basically anything that floats.
The Weight Story
Static intact stability involves two stories. This simply means that the weights side of the story must match the waters side of the story. First, each side of the story will be described, and then the two sides will be combined.
The weight story is described first. In nature each component of weight contributes automatically to the weight of the whole. Each weight has its own center and all the weights combined have a combined center. Determining a vessels total weight (W) and the vertical center of gravity (KG) of all weights present is basically the crux of the weights side of the story.
Here is a simple example. A boat has a hull that weighs 200 pounds. Attached to its transom is a 100 pound outboard. The hulls weight center is 1 foot above the keel. The engines weight center is 2 foot above the same spot on the vessels keel. The calculations required are as follows: Total Weight = W = 200 + 100 = 300 pounds. The sum of vertical moments = VM = 200# x 1 foot + 100# x 2 foot = 400 foot pounds. Vertical Center of Gravity = KG = Vertical Moments divided by Total Weight = VM / W = 400 / 300 = 1.333 feet (or 1 4) above the keel reference point. Normally a vessel consists of hundreds and sometimes thousands of items. Weights and Moments tables are often utilized to determine a vessels total weight and combined center of gravity.
The Water Story
Now lets go to the waters side of the story. The waters story is based on a rocking point that naturally occurs in nature. This rocking point is called the transverse metacenter. This metacenter is labeled as M in Figure A. To obtain the distance KM two items need to be first computed. The first is KB and the second is BM. Both will be explained in following paragraphs.
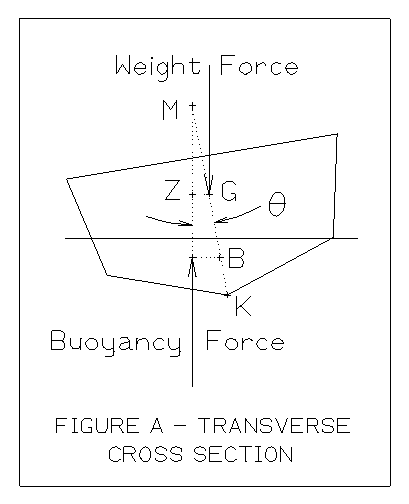
The first thing that needs to be determined is the distance from the vessels center buoyancy to the keel. The symbol for this term is defined as KB. (T in the following formula represents the draft at the Longitudinal Center of Floatation, but the draft at amidships or mean draft should be close enough for estimating purposes. Note also that T is the canoe draft of the hull only, it does not include the effects of keels, skegs or other appendages.) For normal shaped vessels KB can be estimated with Formula A as follows:
Formula A) KB = 0.55T
The transverse moment of inertia of the vessels water plane needs to be computed next. The symbol for moment of inertia is I. The transverse moment of inertia for normal vessel shapes can be easily estimated. Formula B represents this type of moment of inertia calculation. The term CWP is defined as the waterplane coefficient. It can be calculated by dividing the waterplane area, AWP, in square feet, by the waterline length, L, in feet, multiplied by the maximum waterline beam, B, in feet [i. e. CWP = AWP/(LB)]. Note that the value of p normally varies from 0.72 to 0.95. Where a value of 0.72 would apply to a slender vessel and a value of 0.95 applies to fuller barge type shapes.
Formula B) I = (1/12) (CWP)2LB3
The vessels volume, V, also needs to be calculated. The vessels weight can easily be converted into cubic feet through a density adjustment. For salt water the density adjustment is 64 pounds per cubic foot. Formula C can be applied to determine a vessels volume.
Formula C) V = W / 64
The term BM represents the metacentric radius. BM is an extremely important term. It is defined as the vertical distance from the Center of Buoyancy to the Metacenter. The numerical value of BM is obtained through Formula D. Proof for validity of this formula is available in fluid mechanics and naval architectural textbooks.
Formula D) BM = I / V
The distance from the keel to the metacenter KM can now be computed. Formula E is applied to compute this value.
Formula E) KM = KB + BM
In
summary, the waters side of the story requires the computation of KB, I,
V, BM, and KM.
Putting the Two Stories Together
KM ties everything together in that it must be the same for both the weight and the water sides of the story. See Figure B.
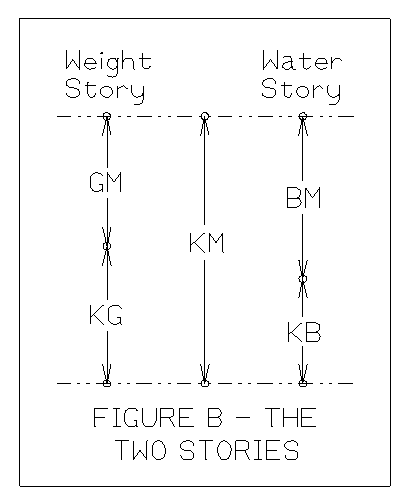
In this figure you see a new term, GM, on the weight side of the story. This term GM is extremely important and it is called the metacentric height of a vessel. For a vessel to be stable the numerical value of GM must be positive. This means that G must always be located below M. GM can be calculated through Formula F as follows:
Formula F) GM = KB + BM - KG
Formula F represents a vessels available GM. The regulations often require a minimum value or values for GM based on other parameters. These parameters usually involve the vessels projected area and may involve other parameters like the quantity of passengers on board. Often a minimum value of 2 is required for GM in a damaged condition. One must refer to the applicable regulations in order to calculate the required GMs for a particular vessel. Then they must be compared against the available GM. The available GM must always be larger than the required GMs. The requirements vary considerably for different types and sizes of vessels. These regulations are self-explanatory so computations for required GM values are not elaborated in this article.
The reason that
metacentric height is so important is because it is directly proportional
to the amount of righting arm available. This righting arm, GZ,
is illustrated in Figure A. In this figure
q
is the angle of heel. Formula G quantifies this righting arm.
Formula G) GZ = GMsin(q)
In conclusion Figure B summarizes the two stories that must to obtain available GM. Additionally a vessels available GM must be greater than any of the GMs required by the regulations
The formulas provided in this article are for teaching purposes. They also can be used for rough estimating. However, this type of estimating is normally not acceptable to Coast Guard for official stability submittals. Naval architectural computer programs are normally used in conjunction with official submittals. These programs very accurately calculate values of KB, BM, and KM. They also generate other important and often required stability data like Lines Drawings, Curves of Form, Cross Curves of Stability, and Curves of Statical Stability.
Static stability was primarily discussed in this article. This term static is applied as opposed to dynamic stability. Dynamic stability involves righting arms over a large range of heel angles. This type of analysis involves quantification of volumetric centers of heeled displacement volumes. Dynamic stability is also important because it is a measure of a vessels ability to withstand the effects of wind and waves. The Coast Guard also has many regulations that deal with dynamic stability.
Other important concepts like floodable length, damaged stability and free surface effects are not covered here. Even some of the finer points of static intact stability were not covered. The reader is advised to do a further study of these concepts in order to obtain a fuller understanding of this topic.
Note: The formulas provided in this article are for teaching purposes. They are also useful for rough estimating. However, this type of estimating is normally not acceptable to the USCG for stability submittals. (Added to article: Use of templates in this website should be acceptable.)
Recent News: On September 27, 2002 the ocean going ferry Le Joola capsized off the coast of West Africa. The death toll ranges from 1,034 to 1,600 passengers and crew. Uncertainty in the count stems from the fact that many passengers did not have tickets. Tragically many of the passengers were children. This is another painful reminder that stability must continue to remain a high priority in vessel design and operation. From: Article entitled "Major Maritime Disasters Mark the Year," on page 6 of Pacific Maritime magazine, January 2003 issue.
Note: This article describes how to find GM, metacentric height, of a vessel based on weights and moments data and hydrostatics data. This is the method normally employed by designers for a vessel that is "not yet built." But if a vessel already "exists," the metacentric height can be estimated from it's roll period or it can be determined accurately by conducting an inclining experiment (stability test and deadweight survey).
Update: Another article in this website, "Understanding Ship and Boat Trim (Stability & Trim - Part 2)" adapts some of the theory, discussed in this article, to longitudinal stability and how it affects trim. Whereas this article apples to the more critical stability that is in the transverse direction.
Simple box barges also present an interesting way to learn about stability, trim, list, weights and moments. There is an article entitled "Barge Trim, List and Initial Stability (GM - metacentric heights)" that should be helpful.
Understanding the parallel axis theorem is also very useful for both stability and structural analysis. This subject is discussed in an article entitled "Parallel Axis Theorem."
Application: The concepts described in this article are utilized in the following templates:


