|
There are basically only two types of trimming calculations. Other
trimming calculations are just variations of these two fundamental types. In
Case
I you know the vessel's weight and center of gravity (CG) location and you
seek
to find the forward and after drafts. In Case II you know the
forward and after drafts and desire to know the vessel's weight and center
of gravity (CG) location. The simple
approach that is presented here should be readily understandable by anyone
with a basic understanding of algebra and geometry.
This article
should benefit anyone involved with designing or operating any type of
floating vessel. Regulatory agents and classification society
employees also need to understand these methods in order to check various
designs for compliance. This article is also designed to give a good
theoretical understanding of the calculative methodology utilized in the
trim and stability sheets sold on this site.
The vessel's "Curves
of Form" are needed to perform these calculations. No attempt is made
to describe the theory behind or how to construct the "Curves of Form." This article is only concerned with application of "Curves
of Form" data.
Vessel Geometry and Sign Conventions Adopted
Vessel geometry is
defined in figure below. All items are drawn to show the positive
sign conventions adopted for this method.
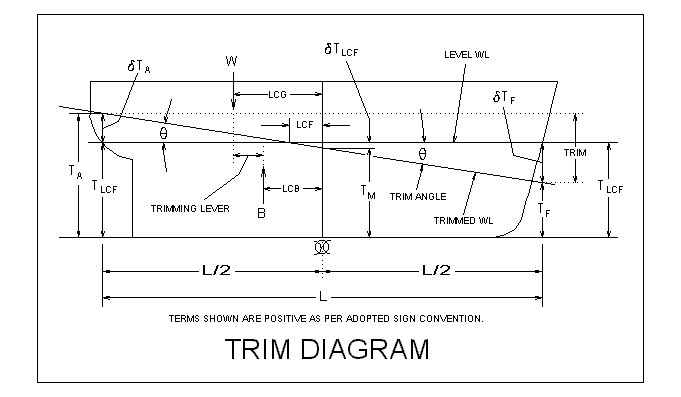
Some important
characteristics of this picture are:
-
B is the Buoyancy Force
provided by the vessel with level trim. Usually
obtained from a "Curves of Form" plot. In this procedure B is
numerically equal to the vessel's displacement (i. e. B =
D).
-
W is the total weight
applied to the vessel. Usually obtained from a
"Weights and Moments"
analysis.
-
L is the
length between the forward and after draft marks
-
LCG is the
Longitudinal Center of Gravity location, normally obtained from a "Weights
and Moments" analysis.
-
LCB is the
Longitudinal Center of Buoyancy location, usually obtained from a "Curves
of Form" plot.
-
LCF is the
Longitudinal Center of Floatation, normally obtained from a "Curves of
Form" plot.
-
TA
is the draft and the Aft Draft marks
-
TF
is the draft at the Forward Draft marks
-
TM
is the Draft Amidships, located midway between forward and aft draft marks
-
TLCF
is the draft located at the Longitudinal Center of Floatation.
The sign
conventions adopted for this presentation are:
-
Distances Aft of
Amidships are Positive, applies to LCG and LCB
-
Trim by the stern
is defined as Positive
-
Trim Moment
causing trim by the stern is Positive
-
Trim Lever that
causes trim by the stern is Positive
Now that the
geometry is defined and the sign conventions are stated, we can proceed
with the two basic trimming cases.
Case I - Displacement & CG Location Known Find Forward
& Aft Drafts
This option is
utilized over and over again in design and operational stages to determine
a vessel's responses to various loading conditions.
Step 1 - Obtain
Equilibrium
-
For
equilibrium the vessel weight must equal the vessel's displacement, W =
D.
-
With this displacement enter the "Curves of Form" and obtain a
draft. This draft (TLCF) obtained is the
draft present at the LCF location.
Step 2 - In the
"Curves of Form" at this LCF draft obtain the following:
-
Moment to Trim
-
MTI Moment
to Trim one Inch, for English Units of long tonsfeet/inch or
-
MTC Moment
to change Trim one Centimeter, for Metric Units of
metric tonsmeters/cm.
-
Longitudinal
Center of Buoyancy, LCB, feet or meters, with aft of amidships
defined as positive
-
Longitudinal
Center of Floatation, LCF, feet or meters, with aft of amidships
defined as positive
Step 4 - Find the
Trim.
-
First the trim
lever is defined mathematically as Trim Lever = LCG - LCB, in
either feet or meters. If this value is positive trim by the stern
should be produced. If it is negative the vessel should trim by the
bow. Sign convention consistency is extremely important. For
instance if the LCG is 5 feet aft of amidships and the LCB is 2 foot
forward, the trimming lever would be equal to 5 - (-2) = positive 7 feet.
Since the numerical value is positive this scenario will cause trim by the
stern.
-
The applied
trimming moment is defined mathematically as TM =
D(LCG
- LCB)
-
The hydrostatic
response trimming moment is defined mathematically as:
-
For equilibrium to
occur, the applied trimming moment must equal the response trimming
moment. The previous defined equations are combined, algebraically
rearranged with the following expressions for trim obtained:
-
TRIM =
D(LCG-LCB)/MTI
for English units of inches, the value obtained must be converted to feet,
by dividing by 12, prior to applying it in the formulas which
follow.
-
TRIM =
D(LCG-LCB)/MTC
for metric units of centimeters, the value obtained must be converted to
meters, by dividing by 100, prior to applying it in the formulas which
follow.
-
When the above
expressions are satisfied, there is corresponding subtle hydrostatic
physical reality for the trimmed vessel condition. This reality is
that the LCB has moved to a new location that is either directly above or
below the LCG location. However, the initial LCB that must be
applied in these trim calculations correspond to the vessel in a level
condition (i. e. obtained from "Curves of Form" values).
Step 5 - Find the
Forward and After Draft Via Geometry
-
This method
involves the use of similar triangles and the position of the LCF.
-
For the forward
draft the similar triangles
present yield the following expression TRIM/L =
dTF/(LCF+L/2),
solve this for dTF
to obtain dTF
= (TRIM/L)(L/2+LCF) = TRIM(1/2+LCF/L), then apply
the following formula from geometry to
obtain the forward draft TF = TLCF -
dTF
= TLCF - TRIM(1/2+LCF/L).
-
For the aft
draft the similar triangles
present yield the following expression TRIM/L =
dTA/(L/2-LCF),
solve this for dTA
to obtain dTA
= (TRIM/L)(L/2-LCF) = TRIM(1/2-LCF/L),
then apply the following formula
from geometry to obtain the forward draft TA
= TLCF + dTA
= TLCF + TRIM(1/2-LCF/L).
-
Alternatively,
based on geometry, the after draft may be more simply computed as
follows:
TA = TF
+ TRIM.
-
With the forward
and aft drafts known the mean draft can be quickly computed as
follows:
TM
= (TF + TA)/2.
Step 6 - Important
Points to Remember
-
If the LCB is aft
of the LCG the vessel will trim by the bow. If the LCB is forward of
the LCG then the vessel will trim by the stern. These principles
apply regardless of the position of the LCF.
-
Sign convention
consistency is extremely important. If they are not followed the
formulas presented here will not work properly.
Step
7 - Improvements Made to this site's Trim and Stability Sheets
-
The MTI or MTC
values that are presented in the "Curves of Form" are based on the
assumption that metacentric radius in the longitudinal direction is equal
to the metacentric height in the longitudinal direction (i. e. BML
= GML). This assumption yields approximations for
moment to trim values. These approximations are normally adequate
since in most cases there is not much difference between the BML
and GML values. Furthermore the approximations must be
made because the VCG values are not known at the time that the "Curves of
Form" are made.
-
However in the
"Trim and Stability Sheets," that are available on this website, the VCG
values are known for the conditions at hand, so the moment to trim values
are computed accurately. Three basic formulas are applied.
First, by definition, the restoring moment = GMLDTanq.
Second geometry present requires that Tanq
= Opposite/Adjacent = TRIM/L. Three, by definition GML =
KML - VCG, where KML is obtained from the "Curves of
Form" instead of MTI or MTC. All three of these equations are
combined and rearranged yielding: MTF = (KML - VCG)D/L.
MTF in this case is moment to trim one foot, where TRIM equals one foot.
Note that ML can be obtained from the following formula: KML
= BML + VCB. The "Curves of Form" may just give BML
and VCB, but this is alright since these can be summed to obtain the KML
value. Another article in this website, "Understanding
Stability" explains the theory discussed in this paragraph.
However, a little adaptation is required by the reader because that
article applies to stability in the transverse direction and this article
applies to stability in the longitudinal direction.
Case II - Forward
& Aft Drafts Known, Find Displacement
& LCG Location
This option is
used by naval architects, yacht and boat designers, marine surveyors,
marine inspectors and others for deadweight surveys and for stability tests.
It is also used by dock masters, by captains, mates, fisherman and others who
may want to determine a vessel's weight and center of gravity location.
The first goal of
this analysis is to find the LCF draft. This draft is needed because
the "Curves of Form" are based on the LCF draft and not the mean draft.
After this draft is determined, the primary goals of obtaining a
displacement and the LCG location are easily determined through the use of
the "Curves of Form" data.
Step
1 - Calculate the Mean Draft & Trim Present
-
Compute the mean
draft present, where TM = 1/2(TF + TA).
Remember the "Curves of Form" are not based on this mean draft but on the
LCF draft. However this mean draft serves its purpose as a close
estimate for the LCF draft and is initially used to retrieve preliminary
data from the "Curves of Form."
-
Compute the trim
present, with this formula TRIM = TA - TF.
-
These values of
draft and trim are now used to help determine the LCF draft (TLCF).
Step
2 - Obtain the LCF Draft Through Iteration
-
At TM go
into the Curves of Form and obtain a
initial value for LCF.
-
An expression for
the LCF draft needs to be derived. Fortuitously the waterline slope
(or Tanq =
TRIM
/
L) and the ship
length (L between forward and aft draft marks) are known. From
similar triangles we have
dTLCF
/ TRIM = LCF / L. From geometry we have TLCF
= TM +
dTLCF.
Combining the preceding two equations we have: TLCF
= TM + (TRIM)LCF / L
-
Compute the
initial guess for LCF draft through application of TLCF
= TM + (TRIM)LCF / L
-
Go back to
the "Curves of Form" with initial TLCF just computed and
obtain a new value for LCF.
-
Recompute the LCF
draft, by using the LCF value just obtained into the following formula:
TLCF = TM + (TRIM)LCF / L.
-
The LCF just
obtained should be close to the one previously calculated. If not,
repeat this process using the most recent LCF draft value to enter the
"Curves of Form" to get a new LCF value. Recompute another LCF draft
using the formula TLCF = TM + (TRIM)LCF / L
and compare it with the preceding LCF draft computed, they now should be
very close. Usually only need to iterate once. The last value
for LCF draft is the considered the actual LCF draft and it is applied in
the rest of this analysis.
Step
3 - Obtain "Curves of Form" Data Based on the LCF Draft
-
With the last TLCF
value enter the "Curves of Form" and obtain the following:
-
Displacement,
D
-
Longitudinal
Center of Buoyancy, LCB
-
Moment to Trim,
MTI or MTC. Which term depends on applicable units
system.
-
MTI
for English units of inches, the value obtained from "Curves of Form" must be converted to feet,
by dividing by 12, prior to applying it in the formulas which
follow.
-
MTC for
metric units of centimeters, the value obtained from "Curves of Form" must
be converted to meters, by dividing by 100, prior to applying it in the
formulas which follow.
Step
4 - Derive Relationships Between Trim and LCG
-
Two relationships
for trimming are presented and then equated to each other, the combined
result is then manipulated to give an expression for computing LCG.
-
First the
applied trimming moment is defined as TM =
D(LCG
- LCB).
-
Second the
hydrostatic response moment is defined as TM = MTITRIM.
-
These equations
are equated to each other and solved for LCG to obtain the following
result:
LCG = LCB + MTI TRIM /
D
Step
5 - Calculate the LCG Value
Step 6 - Important
Points to Remember
-
It trim
value is positive, the vessel is has trim by the stern (the stern is
submerged deeper than the bow) then the LCG must be located aft of the LCB.
-
If trim value is
negative, the vessel has trim by the bow (the bow is submerged deeper than
the stern), then the LCG must be located forward of the LCB.
-
Sign convention
consistency remains extremely important! If they are not followed
exactly the
formulas presented here will not work properly.
Update:
Another article on this website, "Understanding
Ship and Boat Stability (Stability & Trim - Part 1)" is meant
to be a prelude to this article. This article
apples to stability in the longitudinal direction, whereas the prelude
article applies to stability that is in the transverse direction.
Simple box barges also present
an interesting and quick way to learn about stability, trim, list,
weights and moments. There is an article entitled "Barge
Trim, List and Initial Stability (GM - metacentric heights)" that
should be helpful.
Understanding the parallel axis
theorem is also very useful for both stability and structural analysis.
This subject is comprehensively discussed in an article entitled "Parallel
Axis Theorem."
Application:
The concepts described in this article are utilized in the following
templates:
|



